Submit

1 Des 2012

Vektor Pada Sistem Koordinat Ruang ( x, y, z )

.

 

Telah kamu  lihat bagaimana suatu vektor diuraikan atas komponen-komponen pada sumbu x dan sumbu y. Untuk vektor yang terletak dalam ruang (3 dimensi), maka vektor dapat diuraikan atas komponen-komponen pada sumbu x, y dan z.

 

clip_image001

a, b, g = masing-masing sudut antara vektor A

              dengan sumbu-sumbu x, y dan z

clip_image003 = clip_image003[1]x + clip_image003[2]y + clip_image003[3]z

                 atau

clip_image003[4] = Ax  clip_image005+ Ayclip_image007+ Az clip_image009

Ax  = clip_image003[5] cos a

Ay = clip_image003[6] cos b

Az = clip_image003[7] cos g

Besaran vektor A

clip_image011

dan clip_image005[1], clip_image007[1], clip_image009[1] masing-masing vektor satuan pada sumbu x, y dan z

 

 

4. Vektor Satuan

 

Vektor satuan adalah vektor yang besarnya satu.

a.                              clip_image015Penjumlahan Vektor Satuan

   clip_image017     

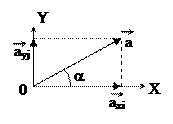
Untuk bidang dimensi 2         v = vxclip_image019                      ®

Untuk bidang dimensi 3         v = vxclip_image021            ®

 

 

Contoh:

            a = 4clip_image023 +2 clip_image025 - clip_image027                 a + b  = ( 4i +2 j - k ) + ( i - j +2 k )

                        b = clip_image023[1] - clip_image025[1]+ 2clip_image027[1]                               = (4 + 1)i + (2 -1)j + (-1 + 2)k

                                                                                = 5 clip_image023[2] + clip_image025[2] + clip_image027[2]

b.                              clip_image028Perkalian Vektor Satuan

Ø  Perkalian titik (dot product)

Arah sumbu x =  clip_image023[3]

Arah sumbu y = clip_image025[3]

Arah sumbu z =  clip_image027[3]

besar clip_image017[1] satuan

 

 

Perkalian titik 2 vektor satuan sejenis             Perkalian titik 2 vektor satuan lain jenis

           clip_image023[4] . clip_image023[5]     = i . i cos q                              clip_image023[6] . clip_image025[4] = i . j cos q                           

                         = 1 . 1 cos 0                                       = 1 . 1 cos 90       

    = 1 . 1 . 1 = 1 satuan                          = 1 . 1 . 0 = 0 satuan

          clip_image025[5] . clip_image025[6]    = 1                                           clip_image025[7] . clip_image027[4] = 0   

           clip_image027[5] . clip_image027[6]    = 1                                          clip_image023[7]. clip_image027[7]   = 0

 
  clip_image029
 


Jika vektor a diuraikan menjadi vektor proyeksinya

 

clip_image030Vektor satuan       ®        clip_image032 = clip_image032[1]xi­ +  clip_image032[2]yj + clip_image032[3]zk

ax 2 + ay 2 + az 2

 
Besar   ®      clip_image032[4]            =  clip_image034

 
  clip_image035
 


Arah ®           tg a     =  clip_image037

Perkalian dot vektor clip_image032[5] dengan vektorclip_image039

 

ax 2 + ay 2 + az 2

 
clip_image032[6] . clip_image039[1]  = clip_image032[7]xi + clip_image039[2]yj     ®               [clip_image032[8] ]     =  clip_image041

bx 2 + by 2 + bz 2

 
                                                [clip_image039[3]]      =  clip_image034[1]

 

Contoh 1:       clip_image032[11] = clip_image023[8]+ 2 clip_image025[8]- 3clip_image027[8]         clip_image032[12] . clip_image039[6] =  (clip_image023[9]+ 2clip_image025[9]- 3k ) . ( -2clip_image023[10] + 5clip_image025[10]- clip_image027[9] )

 clip_image039[7] = -3clip_image023[11]+ 2clip_image025[11]– clip_image027[10]                 =  ( 1 )( -2) + ( 2)(5) + ( -3 )( -1)

                                                                        =  ( -2 ) + ( 10 ) + (3 ) = 11

Contoh 2:                         

Dua vektor p = 3clip_image023[12]- 4clip_image025[12] dan q = 4clip_image023[13]-3clip_image025[13]

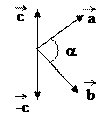
Hitung:            a.  p . q

                        b.  sudut apit antara p dan q

Jawab:

a.             p . q        =  (3clip_image023[14]- 4clip_image025[14]) . ( 4clip_image023[15]-3 clip_image025[15])

                        =  ( 3 )( 4 ) + ( -4 )( -3 ) = ( 12 ) + ( 12 ) = 24

b.            p = clip_image046= 5

q =  clip_image048 = 5

bila sudut apit antara p dan q adalah q, maka

p . q = p q cos q

 

 

cos q       = clip_image050 = clip_image052 = clip_image054 = 0,96

 

q  = 16,26°

 

Ø   Perkalian silang (cross product)

- Perkalian silang 2 vektor satuan sejenis   - Perkalian silang 2 vektor satuan lain jenis

       
  clip_image055   clip_image056
 
 

 

 

 

 

 

 


clip_image023[16]x clip_image023[17]   = 1 x 1 sin q    clip_image025[16]x clip_image025[17]  = 0                   clip_image025[18]x clip_image025[19]  = -clip_image027[11]    clip_image023[18]x clip_image025[20]  = clip_image027[12]

            = 1 x 1 sin 0    clip_image027[13] x clip_image027[14] = 0                   clip_image023[19]x clip_image027[15]  = -clip_image025[21]    clip_image025[22] x clip_image027[16] = clip_image023[20]

            = 1 x 1 x 0 = 0 satuan                         clip_image027[17] x clip_image025[23] = -clip_image023[21]     clip_image027[18] x clip_image023[22] = clip_image025[24]    

 

Memakai Determinan

Contoh:

clip_image057clip_image032[13] = 2clip_image023[23]+ 3clip_image025[25]+ -4 clip_image027[19]         dan             clip_image039[8] = 3 clip_image023[24]-4 clip_image025[26] + 2clip_image027[20]

clip_image032[14] x clip_image039[9] = clip_image023[25](3)(2) + clip_image025[27](-4)(3) + clip_image027[21](2)(4)

           - clip_image027[22](3)(3) - clip_image023[26](-4)(-4) -clip_image025[28](2)(2)

= 6 clip_image023[27]+ (-12) clip_image025[29] + 8 clip_image027[23] - 9 clip_image027[24] + 8 clip_image023[28]- 4clip_image025[30]

= 14clip_image023[29]- 16 clip_image025[31] - clip_image027[25]

Besar   clip_image032[15] x clip_image039[10] =   | a x b |        =   clip_image059 =  clip_image061

Memakai Cara Praktis

 

clip_image062clip_image032[16] = x clip_image023[30]+ y clip_image025[32] + zclip_image027[26]       clip_image039[11] = pclip_image023[31]+ q clip_image025[33] + r clip_image027[27]

                                                            = (y.r – q.z) clip_image023[32]+ (z.p –x.r) clip_image025[34]+ (x.q – y.p) clip_image027[28]

 

Contoh:          

clip_image063clip_image032[17] = clip_image023[33]+ 2clip_image025[35] -3 clip_image027[29]        dan      clip_image039[12]  = -3clip_image023[34]+ 2clip_image025[36] + clip_image027[30]

Jawab:

 

            = (2.1 – 2. -3) clip_image023[35] +(-3.-3  - 1.1) clip_image025[37]+ (1.2 – 2. -3) clip_image027[31]

            = 8 clip_image023[36]+ 8 clip_image025[38] + 8 clip_image027[32]

 

di 4:29 AM

0 komentar:

Posting Komentar